Úvod
Kontrolní metody jsou v podstatě jednoduché metody hospodářské úpravy, odpovídající charakteru výběrného lesa, známé a lokálně uplatňované již déle něž 100 let (POLENO 1999, s. 88). Za jejich zakladatele se považuje GURNAUD. O propracování jeho myšlenek a pracovních metod se zasloužil především BIOLLEY. Tyto metody vycházejí z přesvědčení, že výnos z lesa nelze stanovit dopředu, ale jedině na základě průběhu růstu stromů, jehož zjišťování je třeba periodicky opakovat.
Základem hospodářské úpravy jsou tzv. kontoly, tj. systematická srovnávání vhodně tloušťkově rozčleněných porostních zásob (od stanovené minimální tloušťky stromů – většinou 15 – 16 cm) na pevně vymezených plochách (parcely, oddělení apod.). Srovnáváním a vyhodnocováním pohybu porostních zásob (Z2 – Z1), v souvislosti s provedenými těžbami v kontrolovaném období (T) a dorostem do kmenoviny (D), se sleduje postupné dosažení tzv. ekonomické zásoby. To je porostní zásoba poskytující maximální přírůst (BIOLLEY), popř. maximální přírůstové procento (EBERBACH) a jeho nejvyšší kvalitu. Není přitom rozhodující pouze její výše, ale i její rozčlenění na tloušťkové třídy.
Nástroji hospodářské úpravy při kontrolních metodách jsou přírůst (přírůstové procento), křivka četností výčetních tloušťek a doba přesunu. Tou se rozumí doba (v rocích) potřebná k tomu, aby strom zvětšil svou výčetní tloušťku o počet centimetrů, rovný velikosti intervalu tloušťkových stupňů. Křivka četností výčetních tloušťek by ve výběrném lese měla odpovídat LIOCOURTově zákonitosti – počet stromů od jednoho tloušťkového stupně k následujícímu by se měl snižovat ve stálém poměru (podle LIOCOURTa má tento sestupný koeficient hodnotu 1,3 až 1,5).
Kontrolní metody můžeme rozdělit na:
1. Klasické kontrolní metody
1.1 Výpočet přírůstu „en bloc“
1.2 Výpočet přírůstu po tloušťkových třídách
1.3 Výpočet přírůstu po tloušťkových stupních
Hlavním kontrolním ukazatelem je přírůstové procento, tj. podíl přírůstu a zásoby, na které se přírůst vytvořil, násobený stem. Přírůst se zjišťuje vyhodnocením dvou po sobě následujících inventarizací, a to buď vcelku nebo po tloušťkových třídách, popř. stupních při použití základní přírůstové rovnice: CBPt = (Vt – Vt-n + T – D)/n , kde Vt – zásoba porostu na konci kontrolního období Vt-n – zásoba porostu na počátku kontrolního období T – těžba během kontrolního období D – dorost do kmenoviny (zásoba stromoví, které přerostlo registrační hranici během kontrolního období) n – počet let kontrolního období Představitelé (= zakladatelé kontrolních metod) – GURNAUD, BIOLLEY, TICHÝ a jejich následovníci EBERBACH, KNUCHEL.
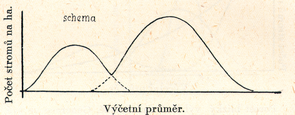
Obr.1: Křivka představuje stejnověký porost s mladou spodní etáží. Pěstební zákrok: vhodně časované prosvětlení etáže vrchní – DOLEŽAL 1948, s. 115.
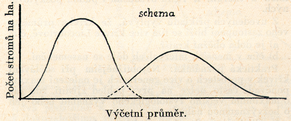
Obr. 2: Porost právě obnovovaný, snad příliš rychle. Pěstební zákrok: propracování středních tloušťkových stupňů – DOLEŽAL 1948, s. 115.
1.1 Výpočet přírůstu „en bloc“
(DOLEŽAL 1948, s. 94) Jedná se o nejjednodušší kontrolní metodu. Příklad: Les H.C., plocha 4,84 ha, období 1920 – 1925
| Rok | počet stromů (ks) | zásoba (sv.) |
| 1920, březen | 1493 | 1638,6 |
| 1921 – těžba | 175 | 243 |
| 1926, březen | 1424 | 1707,4 |
| dorost do kmenoviny | 106 | 25,7 |
| Výpočty | ||
| přírůst „en bloc“ | = 1707,4 – 1638,6 + 243 = | 311,8 |
| „čistý“ přírůst | = 311,8 – 25,7 = | 286,1 |
| roční celkový přírůst | = 311,8 / 5 = | 62,4 |
| roční „čistý“ přírůst | = 286,1 / 5 = | 57,2 |
| přírůst na ha / rok | = 62,4 / 4,84 = | 12,9 |
Poznámka: Jak je patrné, dorost do kmenoviny je nedostatečný, neboť 106 nových stromů nemůže nahradit 175 stromů vytěžených. Z této skutečnosti je nutno vyvodit důsledky při hospodářských úvahách pro příští období.
Další ukázka výpočtu přírůstu „en bloc“ podle GURNAUDa při hospodářské úpravě obecního lesa v Eperonsu (KORF 1955, s. 239).
1.2 Výpočet přírůstu po tloušťkových třídách
Tento postup rozlišuje a pracuje s tloušťkovými třídami, které jsou následující: – silná (tloušťkové stupně 55 – 75 cm, interval 5 cm) – střední (tloušťkové stupně 35 – 50 cm) – slabá (tloušťkové stupně 15 – 30 cm)
Příklad výpočtu přírůstu podle tloušťkových tříd
(podle BORELa, In: DOLEŽAL 1948, s. 96)
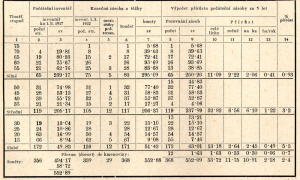
Srovnáme-li součet sloupce č.2 a č.6 zjistíme, že počet stromů v tloušťkové třídě silných vzrostl o 15 stromů (80 – 65). Těchto 15 stromů je tedy nutné připočítat ke tloušťkové třídě středních stromů, neboť z těchto přešly do silných. Proto ve sloupci č.8 odečítáme v součtu oněch 15 stromů tloušťkového stupně 55 a výsledkem je pak součet 65 silných s odpovídající zásobou 250,26 sv.
65 stromů inventáře z roku 1917 vzrostlo tedy během 5 let oběžní doby ze zásoby 239,17 na 250,26 sv a jejich rozdíl dá přírůst celé líchy (parcely). Srovnáme-li konečně roční přírůst tloušťkové třídy silných celé líchy s počáteční zásobou, dostaneme přírůstové procento.
A ještě jedna ukázka výpočtu přírůstu podle tloušťkových tříd (podle metody GURNAUDovy – BIOLLEYovy, In: KORF 1955, s. 246).
1.3 Výpočet přírůstu po tloušťkových stupních
Jedná se o obměnu předcházejícího výpočtu. Zaveden byl BIOLLEYem, inspirován GURNAUDem. Tento postup nejhlouběji představuje myšlenku učení kontrolních metod v její snaze nahlédnout do vývoje celého stromového společenstva.
Příklad výpočtu přírůstu po tloušťkových stupních (GURNAUD): (podle GAZIN, D‘ ALVERNY, SCHÄFFER, In: DOLEŽAL 1948, s. 99)
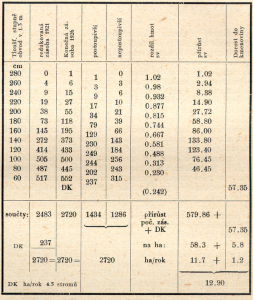
Postup výpočtu se opírá o počty stromů v jednotlivých tloušťkových stupních na počátku a konci inventární periody. Zavádí stromy „postoupivší“ a „nepostoupivší“ do vyššího tloušťkového stupně. Takto je možné získat i přírůstové procento pro tloušťkový stupeň (příp. dobu přesunu). Hodnoty objemových rozdílů byly sestaveny ve zvláštní tabulce, odvozené z lokálního objemového tarifu, pronásobené s počty stromů ve sloupci „postoupivší“ dávají přímo přírůst v určitém tloušťkovém stupni.
2. Kontrolní metody křivkové
2.1 Výpočet počtu stromů podle LIOCOURTova zákona
2.1.1 Praktický postup určení vzorové LIOCOURTovy křivky, výpočtu zásob a těžby
2.2 Výpočet počtu stromů podle MEYERa
Kontrolní metody křivkové odmítají přírůstové procento pro jeho labilitu a za jediný kontrolní ukazatel považují křivku tloušťkových četností. Kontrola na určité plošné jednotce se zakládá na porovnání skutečné křivky četností tloušťek s tzv. křivkou vzorovou. Skutečná křivka tloušťkových četností zobrazuje vztah mezi počtem stromů v jednotlivých tloušťkových stupních a tloušťkovými stupni odvozenými z průměrkování. Vzorová křivka zobrazuje četnosti tloušťek vzorových typů lesa. Odvozena je matematicky, jako sestupná geometrická řada (LIOCOURTův zákon, 1898).
Představitelé – LIOCOURT, SCHAEFFER, GAZIN, D‘ ALVERNY a MEYER.
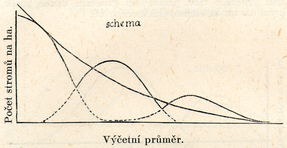
Obr. 3: Porost blízký výběrné kmenovině. Generace ve své posloupnosti se vyrovnávají, vyrovnané blíží se stavu danému křivkou LIOCOURTovou (DOLEŽAL 1948, s. 116)
Definice LIOCOURTova zákona: V každém dokonalém výběrném lese, nalézajícím se v rovnováze, zmenšuje se počet stromů od jednoho stupně tloušťkového k druhému podle stálého poměru. Tuto skutečnost je možno matematicky zapsat:
Nn = a . q-(n-1) , kde
Nn – počet stromů příslušného tloušťkového stupně ni
a – maximální počáteční četnost v prvním tloušťkovém stupni
q – kvocient geometrické řady
n – počet tloušťkových tříd
Tyto hodnoty je možné zjistit pouze výpočtem z empiricky určených křivek tloušťkových četností v porostech. Pochopitelně, takovýchto vzorových křivek existuje větší množství, pro různé typy výběrných lesů.
MEYER vyjádřil stromovou četnost ve výběrném lese jako funkci výčetní tloušťky pomocí přirozeně exponenciální funkce ve tvaru:
y = k . e-a . x , kde
y – počet stromů v tloušťkovém stupni
k, a – konstanty, charakterizující křivku stromových četností a tím i specifický výběrný les
e – základ přirozených logaritmů
x – výčetní tloušťka (tloušťkový stupeň)
2.1 Výpočet počtu stromů podle LIOCOURTova zákona
Příklad výpočtu počtu stromů v jednotlivých tloušťkových stupních na základě LIOCOURTova zákona
Vycházíme z toho, že úbytek stromů v tloušťkových stupních lze vyjádřit geometrickou řadou:
a, a.q-1, a.q-2, a.q-3, …………… , a.q-(n-1) , tedy že platí vztah: a = qn .
Zadání příkladu:
a = 82, n = 11, střed první tl. třídy = 20 cm, interval = 5 cm, q = n-tá odmocnina z „a“ = 1,493 = 1,5.
Vypočtěte počty stromů v následujících tloušťkových stupních.
| číslo tl. třídy | tl. třída (cm) | vzdálenost od 1. stupně | pořadí | výpočet | počet stromů (ks) |
| 1 | 20 | n-11 | 0 | 82 | 82 |
| 2 | 25 | n-10 | 1 | 82/1,5^1 | 55 |
| 3 | 30 | n-9 | 2 | 82/1,5^2 | 36 |
| 4 | 35 | n-8 | 3 | 82/1,5^3 | 24 |
| 5 | 40 | n-7 | 4 | 82/1,5^4 | 16 |
| 6 | 45 | n-6 | 5 | 82/1,5^5 | 11 |
| 7 | 50 | n-5 | 6 | 82/1,5^6 | 7 |
| 8 | 55 | n-4 | 7 | 82/1,5^7 | 5 |
| 9 | 60 | n-3 | 8 | 82/1,5^8 | 3 |
| 10 | 65 | n-2 | 9 | 82/1,5^9 | 2 |
| 11 | 70 | n-1 | 10 | 82/1,5^10 | 1 |
2.1.1 Praktický postup určení vzorové Liocourtovy křivky, výpočtu zásob a těžby
Příklad: Dimenze mýtního typu = 66 cm. Počáteční tloušťkový stupeň (střed) = 10 cm. Interval tloušťkového stupně = 4 cm. Stanovte vzorovou Liocourtovu křivku, zásobu a těžbu.
Blíže viz. níže uvedený obrázek. (LESOPROJEKT, Technická príručka, Zvolen, 1984, s. 356)
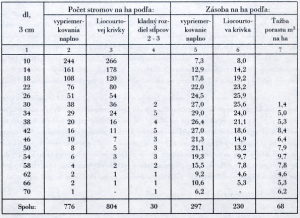
Nejdříve stanovíme počet tloušťkových stupňů od tloušťkového stupně, do něhož spadá předem stanovená dimenze mýtního typu, do počátku, tj. do počátečního tloušťkového stupně. Dostáváme hodnotu 15 tloušťkových stupňů.
Předběžně LIOCOURTovu křivku stanovíme podle tabulek. Snažíme se v této tabulce ve sloupcích, které odpovídají tloušťkovým stupňům 10 – 22 cm (v tabulce to odpovídá sloupcům 15 – 12) vyhledat ten řádek, který se bude z pohledu množství skutečného počtu stromů z vyprůměrkování naplno co nejvíce přibližovat údajům v tabulce. Takto se dostáváme na řádek s koeficientem klesání „q“ = 1,48.
V této tabulce u tohoto koeficientu klesání je však hodnota celkového počtu stromů na 1 ha rovna 743 kusům. To je o 33 kusů méně než jich ale máme podle údaje z průměrkování naplno. Z tohoto důvodu výslednou LIOCOURTovu křivku odvodíme tak, aby součet stromů byl nejblíže vyšší než je údaj z průměrkování naplno. Proto výsledná LIOCOURTova křivka se bude řídit podle koeficentu klesání = 1,49 (celkový počet stromů = 804).
Následně určíme vyrovnanou (vzorovou) LIOCOURTovu křivku zásoby. Vyjdeme z poměru mezi počtem stromů z vyrovnané křivky a skutečným počtem stromů z vyprůměrkování naplno po jednotlivých tloušťkových stupních. Například v 1. tloušťkovém stupni tento poměr činí 1,1 (266/244). Hodnotu zásoby v tomto tloušťkovém stupni (7,3) pak násobíme koeficientem 1,1, čímž dostáváme pro tento tloušťkový stupeň velikost zásoby podle LIOCOURTovy křivky rovnu 8,0 m3 na 1 ha, atd. po dalších tloušťkových stupních.
Určení těžby provedeme výpočtem u těch tloušťkových stupňů, u kterých počet stromů z vyprůměrkování naplno převyšuje počet stromů odvozený z LIOCOURTovy křivky. K tomuto nutně potřebujeme znát průměrnou hmotnatost jednotlivých tloušťkových stupňů. Tu vypočteme podílem zásoby a počtu stromů z vyprůměrkování naplno. Například pro tloušťkový stupeň 30 cm činí jeho průměrná hmotnatost 0,711 m3 (27/38). Protože máme vypočteno, že v tomto tloušťkovém stupni nám oproti vyrovanému stavu nadbývají 2 stromy, navrhneme je k těžbě, pak objem těžby naplánovaný v tomto tloušťkovém stupni bude činit 1,4 m3 (2 * 0,711) na 1 ha, atd. adekvátně provedeme výpočet po následujících tloušťkových stupních. Na celý porost naplánujeme takto vytěžit 68 m3.
2.2 Výpočet počtu stromů podle MEYERa
(blíže k odvození výpočtu, např. KORF 1955, s. 182 – 184) Základní parametry rovnice pro výpočet počtu stromů podle základních typů výběrných lesů (A-E):
| Veličina | Typ výběrného lesa | ||||
| A | B | C | D | E | |
| a | 0,055 | 0,060 | 0,065 | 0,070 | 0,075 |
| k | 41,4 | 56,5 | 71,7 | 86,9 | 102,1 |
| počet stromů – ks / ha | 300 | 350 | 381 | 398 | 405 |
| výčetní kruhová základna – m2 / ha | 28,2 | 31,0 | 31,8 | 31,4 | 30,3 |
Počty stromů po jednotlivých tloušťkových stupních a podle typů výběrných lesů pak vypadají na základě výše uvedeného následovně (KORF 1955, s. 186). Nutno však vzít v úvahu, že odstupňování typů výběrného lesa(ů) má lokální charakter a tedy, že platí jen pro konkrétní růstovou oblast!
2.2.1 Určení výše těžby
Rozdělení počtu stromů po tloušťkových stupních se však následkem tloušťkového přírůstu každoročně mění o hodnotu, která se rovná průměrnému tloušťkovému přírůstu tloušťkových stupňů. Následkem toho, počet stromů v tloušťkových stupních stoupne, a má-li se obnovit původní rozdělení (na vzorovou křivku), musí se vytěžit počet stromů, který je roven jeho ročnímu nebo periodickému navýšení. Na této úvaze založil MEYER svoji metodu procentuálního navýšení zásoby následkem tloušťkového přírůstu (di) při určitém rozdělení počtu stromů, které je charakterizováno kvocientem „q“ (viz. LIOCOURTův zákon). Hodnoty procentuálního navýšení počtu stromů v závislosti od di a q jsou tabelované, což velmi usnadňuje praktický výpočet těžby v jednotlivých tloušťkových stupních (PRIESOL, POLÁK 1991, s. 225). Shrnuto a podtrženo: Má-li se tedy zachovat původní struktura výběrného lesa, není možné těžit objemový přírůst tloušťkových stupňů, ale právě toto procentuální navýšení zásoby!
3. Doba přesunu
3.1 Výpočet doby přesunu metodou D´ ALVERNYho
3.2 Výpočet doby přesunu metodou podle MEYERa
Definice: Jedná se o dobu v rocích, které je zapotřebí, aby určitý strom zvětšil svůj výčetní průměr o počet centimetrů, který je roven velikosti zvoleného tloušťkového intervalu. Doba přesunu je pravděpodobný čas, za který se všechny stromy přesunou ze současného tloušťkového stupně do tloušťkového stupně vyššího. Tedy, čím je doba přesunu delší, tím pomaleji stromy rostou a naopak. Doba přesunu je tedy v přímém vztahu s tloušťkovým přírůstem a tedy, de facto, nahrazuje informaci o přírůstu stromů. Vypočítá se podle údajů počtu stromů, které se za inventarizační období do vyšších stupňů přesunuly. Několik pravidel použití doby přesunu (DOLEŽAL 1948, s. 178): 1. Ve výběrném lese klesá pravidelně doba přesunu od slabých k silným. 2. Pokles se vyrovnává a zmenšuje správným provedením selekce jedinců v porostním inventáři. 3. Zvětšení doby přesunu u tloušťkových stupňů třídy silných ukazuje na jejich nesprávný výběr, jedná se o stromy přestárlé, nezdravé nebo v korunách se tísnící. 4. Třída slabých a silných vykazuje růst uspokojující, třída středních prodlužování doby přesunu; v této třídě nastává stav tísně, nezbytnost probírky ve třídě středních. 5. Stromy v třídě středních nejsou vždy stromy mladé, jsou to často nevrůstavé stromy stejného věku jako třída silných: nutný zásah výběrem těchto. Délka doby přesunu by se měla pohybovat v rozmezí od 10 let (dobré půdy) do přibližně 20 let (poměry špatné) – DOLEŽAL 1948, s. 150.
3.1 Výpočet doby přesunu metodou D´ ALVERNYho
(DOLEŽAL 1948, s. 141) Výpočet vychází z předpokladu, že množství stromů, které postoupilo do následujícícho (vyššího) tloušťkového stupně je úměrné jejich průměrné rychlosti růstu. Je založen na základě následujícího vztahu: B : O = A : P P = A/B . O , kde A – průměr počtu stromů v témže tloušťkovém stupni na počátku a konci inventarizačního období B – průměr počtu stromů postoupivších z tloušťkového stupně nejblíže nižšího a stupně uvažovaného O – období kontrolní (doba oběžní) P – doba přesunu Kvůli zjednodušení výpočtu se zavádějí následující veličiny: E – dvojnásobný přesun, tj. součet počtu stromů jednoho tloušťkového stupně na počátku a konci inventarizačního období C – součet postoupivších stromů v tloušťkovém stupni nejblíže nižším a uvažovaném P = E/C . O
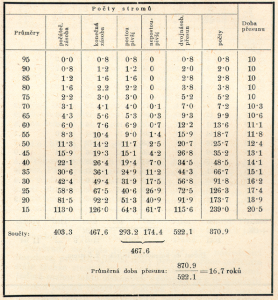
Předpokladem pro tento výpočet doby přesunu je krátké kontrolní období, v němž žádný strom nepostoupí o více než jeden tloušťkový stupeň.
3.2 Výpočet doby přesunu metodou podle MEYERa
(KORF 1955, s. 251) Postupuje-li z celkového počtu stromů v tloušťkovém stupni v „a“ letech „x %“ stromů do následujícího tloušťkového stupně, bude – při stejnoměrném rozdělení stromů uvnitř tloušťkového stupně – pravděpodobná doba, během níž se všechny stromy přesunou, dána jednoduchým vztahem:
P = a/x . 100 roků
Při výpočtu doby přesunu na základě dvou inventarizací a těžby podle tloušťkových stupňů se údaje sestaví tak, jak uvádí následující tabulka (postup setřídění dat v ní podle KNUCHELa):
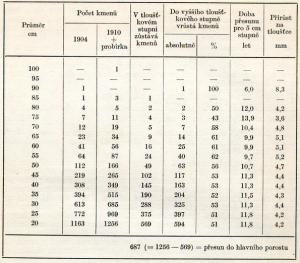
Pro každý tloušťkový stupeň se vypočítá procentický podíl „x“, tj. počet stromů, jež během „a“ se přesunou do následujícího tloušťkového stupně. Z tohoto podílu je pak možno podle výše uvedeného vztahu vypočítat pro jednotlivé tloušťkové stupně doby přesunu a z nich pak například i tloušťkové přírůsty (i):
i = 5cm / P
Když například v tloušťkovém stupni 40 cm ze 308 stromů za 6 let postoupí do tloušťkového stupně 45 cm celkem 163 stromů, tj. 53 %, pak všech 308 stromů postoupí za 11,3 roku (6/53 . 100) a tloušťkový přírůst bude 0,44 cm (5/11,3).
I zde platí, že předpokladem pro tento výpočet doby přesunu je krátké kontrolní období, v němž žádný strom nepostoupí o více než jeden tloušťkový stupeň.
4. Kontrolní metody hodnotové – kvalitativní inventarizace
Představitelé – ARNSWALD, KRUTZSCH-LOETSCH, SPEIDEL, KIRCHNER a PRIESOL.
5. Domácí kontrolní metody
Představitelé – TICHÝ, KUBELKA, NIMBURSKÝ a ŠAŠEK