1. Teorie normálního lesa
2. Model holosečného lesa
2.1 Normální počet a rozloha věkových tříd
2.2 Normální prostorové uspořádání věkových tříd
2.3 Normální přírůst, který odpovídá plnému zakmenění
2.3.1 Znázornění vývoje zásoby a přírůstů zásoby normálního hospodářského souboru
2.4 Normální zásoba
2.5 Normální etát
1. Teorie normálního lesa
Téměř od počátku hospodářské úpravy lesů bylo její zaměření orientováno především na definování stavu lesa, který by byl schopen zabezpečit nepřetržitou a vyrovnanou těžbu (výnos). Vytvořila se tak představa normálního či vzorového lesa.
Pojem normálního lesa byl ze začátku spojován s představou ideálního lesa, který je obhospodařován holosečným hospodářským způsobem. Postupně byla tato představa doplňována o úpravu lesů výběrných. Později se však ukázalo, že formám podrostního hospodářství nevyhovuje ani jedna z výše uvedených modelových představ, a proto byl vypracován i model lesa podrostního.
Obecně je možno konstatovat, že normální les je modelem hospodářského souboru, který má zabezpečit nepřetržitost a vyrovnanost výnosu (těžeb).
2. Model holosečného lesa
Model holosečného lesa je spojován s podmínkami, které formulovali HUNDESHAGEN (1826) a HEYER (1841). Abychom mohli o daném hospodářském souboru hovořit jako o lese normálním je zapotřebí, aby vyhovoval následujícím podmínkám:
- normální počet a rozloha věkových tříd
- normální prostorové uspořádání věkových tříd
- normální přírůst, který odpovídá plnému zakmenění
- normální zásoba
- normální Etát
Takto definovaný normální les bývá také označován jako les tabulkový, neboť jeho produkční vývojový proces má být zachycen v růstových tabulkách. Dále se předpokládá, že je tvořen z porostů stejnověkých, stejnorodých a normálně zakmeněných, jehož jednotlivé věkové třídy jsou normálně (rovnoměrně) plošně zastoupeny. Již z napsaného je evidentní, že tato představa je představou ideální a tudíž nedosažitelnou. Dokonce bývá uváděno, že nejen z hlediska stability, ale i produkce je považován za les nevyhovující. Přesto se však do dnešní doby v lesním hospodářském plánování některých jeho prvků používá (např. normální zastoupení věkových stupňů či normální paseka).
2.1 Normální počet a rozloha věkových tříd
Normální počet věkových tříd hospodářského souboru (m) závisí na době obmýtí (u) a počtu let věkové třídy (n); je tedy dán výrazem:
Normální rozloha ročníku věkové třídy (pi) závisí na velikosti hospodářského souboru (P) a době obmýtí (u). Je tedy možno psát
Abychom získali velikost normální věkové třídy (Pm) je nutno výše uvedený výraz vynásobit ještě počtem let věkové třídy (n), tedy:
Z uvedeného vyplývá, že všechny věkové třídy normálního lesa mají stejnou plochu. Porovnání skutečného a normálního zastoupení věkových tříd je možno využít k posouzení těžebních možností lesa.
2.2 Normální prostorové uspořádání věkových tříd
Za normální prostorové uspořádání věkových tříd normálního lesa bývá považováno takové, které nejlépe vyhovuje podmínkám pěstování, ochrany a těžby dřeva. Nicméně je však nutno si uvědomit, že tento model se vztahuje pouze na velkoplošné hospodářství stejnověkých a stejnorodých porostů. V těchto porostech je normální uspořádání věkových tříd zaměřeno výlučně na ochranu proti převládajícím větrům. Proto za normální prostorové uspořádání věkových tříd bývá z tohoto pohledu označováno takové, které umožňuje těžbu proti směru převládajících větrů tak, aby otevřená porostní stěna byla chráněna.
2.3 Normální přírůst
Za normální přírůst bývá označován maximální přírůst za daných stanovištních podmínek při plném, tj. normálním zakmenění.
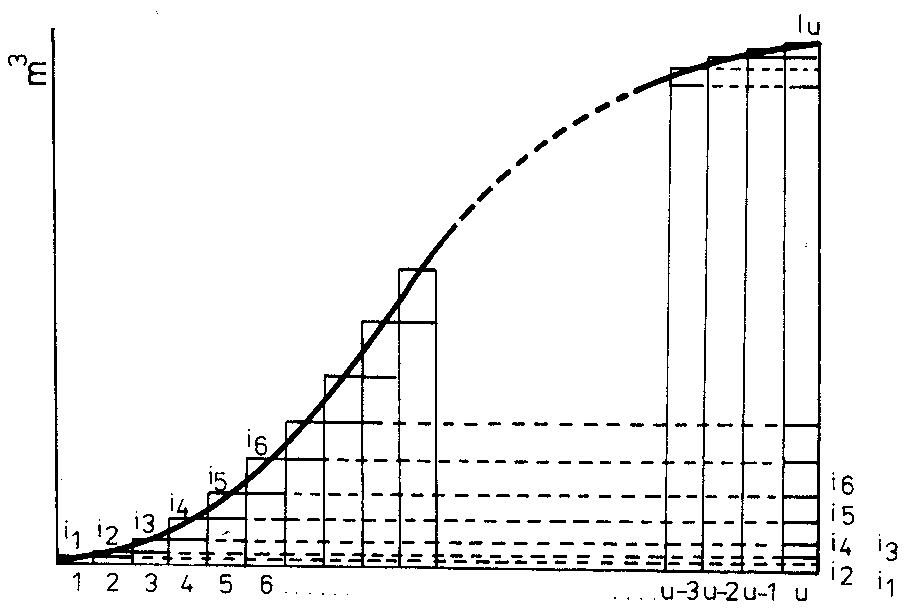
Normální přírůst hospodářského souboru (I) je dán součtem běžných ročních přírůstů jednotlivých ročníků normálního lesa i1, i2, i3 … iu do ročníku doby obmýtí (u). Takto je možno normální přírůst vyjádřit následujícím výrazem:
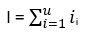
Dále je možno konstatovat, že normální přírůst hospodářského souboru (I) hlavního porostu je roven zásobě posledního věkového ročníku (Vu), tedy že
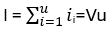
Platí-li, že I = Vu, pak je zároveň možno psát, že I = PMP. To znamená, že běžný přírůst hospodářského souboru v době obmýtí se rovná průměrnému mýtnímu přírůstu (PMP). Stejný závěr pak platí i pro přírůsty celkové objemové produkce, tj. CBP a CPP.
2.3.1 Znázornění vývoje zásoby a přírůstů zásoby normálního hospodářského souboru
2.4 Normální zásoba
Normální zásoba (Vn) vznikne jako součet zásob všech porostů tvořících normální hospodářský soubor. Aby došlo k jejímu vytvoření, je nutné, aby byly splněny výše uvedené tři podmínky fungování normálního lesa, tj. normální počet a rozloha věkových tříd, jejich normální prostorové uspořádání a normální přírůst.
K vyjádření velikosti normální zásoby hospodářského souboru existuje celá řada nejrůznějších vzorců. Z těch nejzákladnějších je možno uvést například výpočet podle PMP, Singera nebo podle Presslerovy lichoběžníkové metody:
| výpočet podle PMP | V = I/2 + I * u/2 |
| výpočet podle Singera | Vn = u/4 * vu + 2vu/2 |
| výpočet podle Presslerovy lichoběžníkové metody | Vn = n(vn + v2n + v3n + … vu/2) |
Blíže odkazujeme na publikaci Hospodárska úprava lesov (Priesol, Polák 1991), strany 216-218.
2.5 Normální etát
Normální etát (E) normálního hospodářského souboru představuje takové množství zásoby, které je možno z něho ročně vytěžit. Již výše byla uvedena zásada, podle které je možno každoročně z lesa vytěžit pouze tak velkou zásobu, která se rovná velikosti přírůstu, tedy